Splitting for planning
A divide-and-conquer approach to plan under constraints - by Panagiotis Grontas
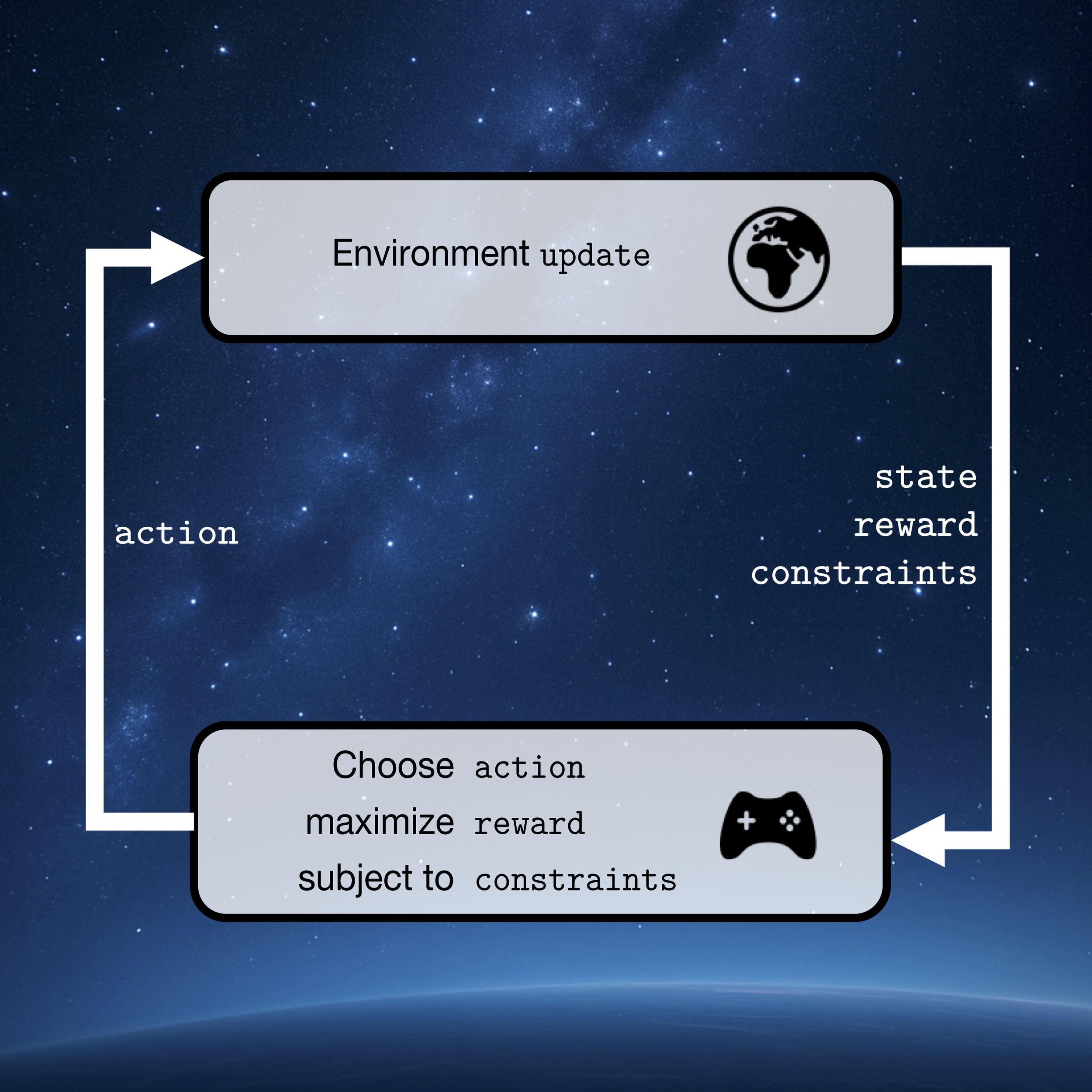
So, what are MDPs? MDPs look a lot like a video game:
We have an intelligent agent that reads the state of its environment (the screenshot of your video game). Based on the state, the agent takes an action (the buttons of your controller).
As a result, the state changes and the agent gets a reward (the screenshot updates and your score increases).
Once the environment the actions, and the rewards are given, MDPs can tell us how the agent should act, given the state of the environment, in order to maximize its reward. Using this game formalism, MDPs have been used to solve extremely difficult planning tasks: from games (like playing chess at a superhuman level), to real-world problems (like warehouse logistics), to futuristic applications (like the control of fusion reactors).
Our life is filled with (boring) planning tasks. Planning is the art of balancing the immediate and long-term effects of our actions, especially when the future is uncertain. Typically, this balancing of short-term and long-term is done according to some notion of reward.
Imagine you are a student and studying leads you closer to graduation in the long term, yet strips away some joys of life in the short term. How do you mediate today’s sacrifice with tomorrow’s reward?
One mathematical tool to answer such questions is Markov Decision Processes, or MDPs for short.
A critical ingredient in the success of MDPs is correctly describing their end goal, i.e. the reward. Yet, defining a reward can be challenging when trying to satisfy multiple conflicting specifications:
In the previous example, our student tries to maximize academic progress, but should keep sleep deprivation to a minimum and coffee consumption to a maximum.
Closer to the real world, a warehouse manager makes monthly plans to maximize profit by ordering/storing/selling products, but should not exceed the capacity limitations of her warehouse.
Notice that some specifications arise as rewards (progress, profit), while others appear as constraints (sleep, coffee, capacity). Our goal is to maximize reward while respecting constraints. Unfortunately, adding constraints to MDPs makes them drastically more complex and difficult to solve.
To address this problem, we apply a divide-and-conquer approach. In a nutshell, our method proceeds by alternating two simple steps:
we teach a greedy agent to obtain reward from the MDP;
we teach a safe agent to respect constraints. Then, we get the
best of both worlds by appropriately combining the behavior of the two agents. In our student’s example, this means finding the optimal proportion of studying, sleeping, and drinking coffee. Maybe answering this question is what motivated us in the first place?
Text by Panagiotis Grontas; illustration created with Microsoft Powerpoint and ChatGPT 
A divide-and-conquer approach to plan under constraints - by Panagiotis Grontas